Les lois de l'algèbre de Boole
L'algèbre de Boole, développée par le mathématicien anglais George Boole au 19ème siècle, est un système mathématique qui traite des opérations logiques sur des variables booléennes, qui ne peuvent prendre que deux valeurs : 0 (faux) et 1 (vrai). Les lois de l'algèbre de Boole définissent les règles qui gouvernent les opérations booléennes et permettent de manipuler et simplifier des expressions booléennes.
Comme nous l'avons vu dans l'article précédent
Algèbre de Boole et simplification des expressions algébrique, l'algèbre booléenne joue un rôle crucial dans l'électronique numérique.
Elle permet de modéliser le comportement des circuits logiques, qui sont les
éléments fondamentaux des ordinateurs et d'autres systèmes numériques.
Dans cet article, nous allons explorer les lois fondamentaux de l'algèbre
booléenne et découvrir ses applications pratiques en électronique numérique.
Loi de commutativité en algèbre de Boole
La loi de commutativité en algèbre booléenne stipule que l'ordre des variables dans une expression booléenne n'affecte pas le résultat de l'opération. En d'autres termes, on peut permuter les variables sans modifier la valeur de l'expression.
La loi de commutativité en algèbre booléenne peut s'appliquer à des expressions booléennes plus complexes, impliquant plusieurs variables et des parenthèses.
Loi d'Associativité en algèbre de Boole
la loi d'associativité en algèbre booléenne stipule que le regroupement des variables dans une expression booléenne n'affecte pas le résultat de l'opération. En d'autres termes, on peut regrouper les variables de différentes manières sans modifier la valeur de l'expression.
Loi de Distributivité en algèbre de Boole
la loi de distributivité est à la base de nombreux théorèmes et identités en
algèbre de Boole, qui sont utilisés pour analyser et manipuler des expressions
booléennes.
La loi de distribution en algèbre de Boole est analogue à celle de l'algèbre
ordinaire. Elle permet de décomposer une expression booléenne en distribuant
un facteur commun. En d'autres termes, elle permet de transformer une
conjonction logique ("et") en plusieurs disjonctions ("ou") ou inversement.
vec les lois et théorèmes introduits dans les articles précédents, il est possible de simplifier n'importe quelle expression booléenne à sa forme la plus simple. Cependant, lors de l'utilisation de l'algèbre booléenne, on rencontre fréquemment des expressions récurrentes. Ces expressions peuvent être considérées comme des règles générales à appliquer directement, mais il est important de comprendre leur origine. Dans les prochains articles, nous présenterons les preuves sous forme d'exercices. Découvrons maintenant les règles de l'algèbre de Boole
Lois de De Morgan
En effet, malgré toutes les lois et règles que nous avons vues jusqu'à présent, il n'est pas toujours possible de simplifier certaines expressions booléennes à leur forme la plus simple.** C'est là qu'intervient la loi de De Morgan, qui apporte une contribution majeure à l'algèbre booléenne en nous offrant un outil puissant pour simplifier davantage les expressions complexes.
La loi de De Morgan joue un rôle crucial dans l'algèbre booléenne en établissant un lien fondamental entre les opérateurs logiques "et" (conjonction) et "ou" (disjonction), et en offrant des outils puissants pour simplifier des expressions.
La loi de De Morgan ne se limite pas à simplifier les expressions booléennes en regroupant les termes négatifs. Elle s'avère également très utile pour décomposer les négations étendues qui s'appliquent à des expressions complexes.





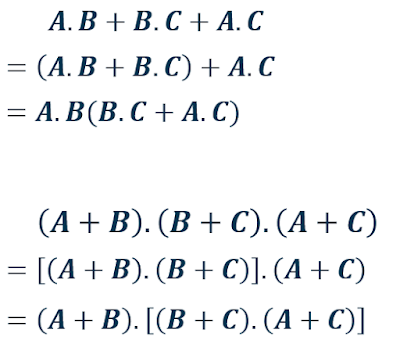




Enregistrer un commentaire